
QTM 350: Data Science Computing
Topic 02: Computational Literacy, Command Line, and Version Control
January 23, 2024
Topic Overview
Computational Literacy
- Binary and Hexadecimal numbers
- Characters, ASCII, Unicode
- High vrs low level programming languages
- Compiled vs interpreted languages
Command Line
- Shell basics
- Help!
- Navigating your system
- Managing your files
- Working with text files
- Redirects, pipes, and loops
- Scripting
Version Control
- Data Science Workflow
- Reproducibility
- Git and GitHub
Computational Literacy
Historical Context
What is a Computer?
What is a Computer?
- Historically, a computer was a person who makes calculations, especially with a calculating machine.
- To do calculations we use numbers. How to represent them?
Representing numbers
Simplest ways to physically represent numbers for arithmetic:
Early mechanical calculators
Four-species mechanical calculators

The first four-species calculating machine, which means that it is able to perform all four basic operations of arithmetic.
Built by Gottfried Wilhelm Leibniz in 1694.
If you took a statistics course before late 1970’s, you may have found yourself using this sort of mechanical calculator.
Silicon Microchip Computers

The 1970s marked the transition from mechanical to electronic:
Transistors act as switches for electronic signalsIntegrated circuits on silicon microchipsVon Neumann architecture revolution
Von Neumann Architecture
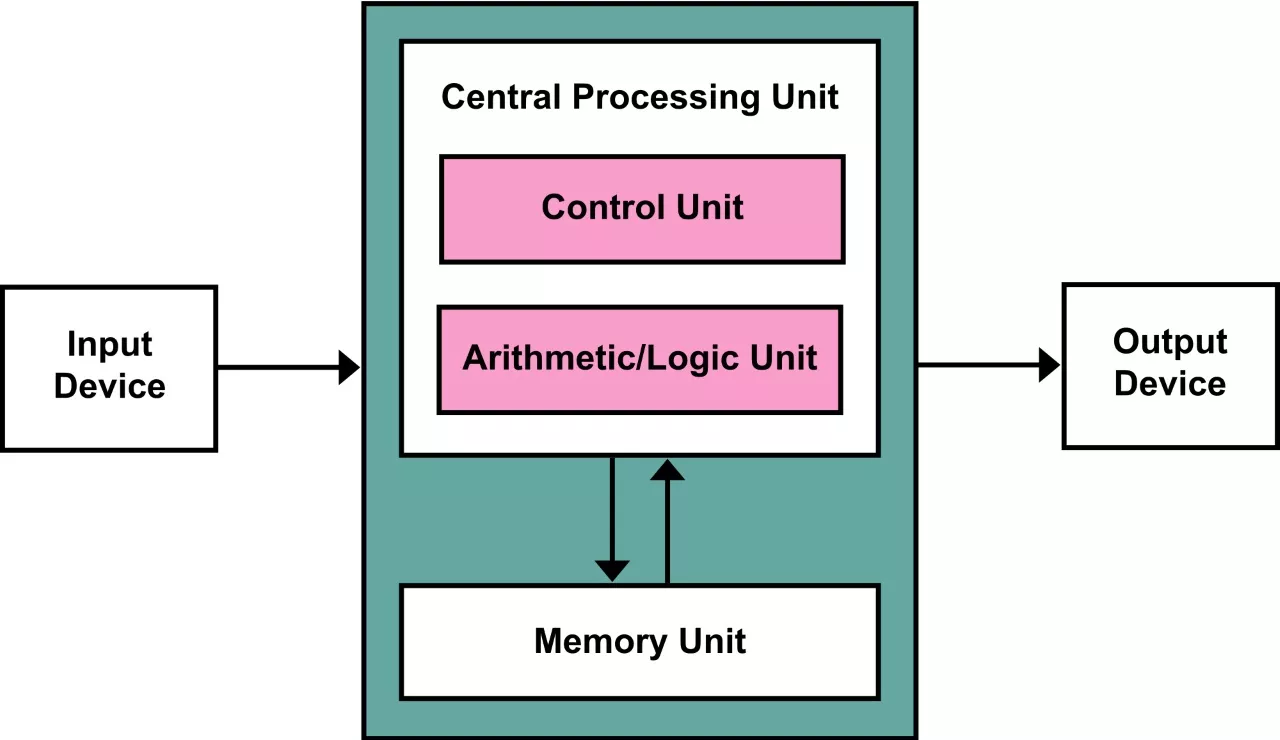
Main feature: the program and any data are both stored together, usually in a slow-to-access storage medium such as a hard disk, and transferred as required to a faster, and more volatile storage medium (RAM) for execution or processing by a central processing unit (CPU).
Since this, it is how practically all present day computers work, the term “Von Neumann architecture” is rarely used now, but it was in common parlance in the computing profession through to the early 1970s.
When Von Neumann proposed this architecture in 1945, it was a radical idea. Prior to then, programs were viewed as essentially part of the machine, and hence different from the data the machine operated on.
Binary Numbers
Introduction to Binary

In modern digital computers, transistors act as switches, with 1 for high voltage level and 0 for low voltage level.
Computers use binary because transistors are easy to fabricate in silicon and can be densely packed on a chip.
What is Binary?
A binary number is written using only the digits 0 and 1.
A single binary digit is a bit, e.g., 101 has three bits.
An 8-bit group is called a byte.
Binary numbers grow as follows:
- 0 represents zero
- 1 represents one
- 10 represents two
- 100 represents four
- 1000 represents eight, and so on…
Binary for Decimal 3
Question: What binary number represents 3?
- 101
- 11
- 111
- 010
Binary Number for Decimal 3
Question: What binary number represents 3?
- 101
- 11
- 111
- 010
Answer: b. 11
- In binary, the number 3 is represented as 11, which equates to \((1 \times 2^1) + (1 \times 2^0)\).
Practice Exercise:
What binary number represents 5?
What binary number represents 7?
What binary number represents 9?
What binary number represents 11?
Machine Code

Machine code or binary code is binary instructions that a CPU reads and executes, such as: 10001000 01010111 11000101 11110001 10100001 00010110.
Early programming was done directly in machine code!
Distinct Numbers in a Byte
Question: How many distinct numbers are represented by a byte?
- \(2^{8}-1\)
- \(2^8\)
- \(2\)
- \(2^7\)
Distinct Numbers in a Byte
Question: How many distinct numbers are represented by a byte?
- \(2^{8}-1\)
- \(2^8\)
- \(2\)
- \(2^7\)
Answer: B) \(2^8\)
- A byte consists of 8 bits.
- Each bit has two possible values (0 or 1).
- Therefore, a byte can represent \(2^8\) or 256 distinct numbers, ranging from 0 to 255.
Converting Instructions into Binary & Understanding ASCII
Characters and Glyphs
- A character is the smallest component of text, like A, B, or /.
- A glyph is the graphical representation of a character.
- In programming, the display of glyphs is typically handled by GUI (Graphical User Interface) toolkits or font renderers.
Converting instructions into Binary
ASCII - The Basics
- ASCII stands for American Standard Code for Information Interchange.
- Standardized in 1968, it defines numeric codes for characters, ranging from 0 to 127.
- Each character is assigned a unique numeric code value.
ASCII Codes
- ASCII defined numeric codes for various characters, with the numeric values running from 0 to 127. For example, the lowercase letter ‘a’ is assigned 97 as its code value.
- Uppercase ‘A’ is represented by the code value 65.
- The code value 0 is the ‘NUL’ character, also known as the null byte.
ASCII Character Range
- Control characters: Codes 0 through 31 and 127 are unprintable.
- Spacing character: Code 32 is a nonprinting space.
- Graphic characters: Codes 33 through 126 are printable.
ASCII Limitations
- ASCII only includes unaccented characters.
- Languages requiring accented characters cannot be represented.
- Even English needs characters like ‘é’ for words such as ‘café’.
Practice Exercise
Write the characters of your name using ASCII codes.
Practice Exercise
Here we have an online translator!
‘DAVI’ using ASCII codes.
| Character | ASCII Code |
|---|---|
| D | 68 |
| A | 65 |
| V | 86 |
| I | 73 |
Note: If ASCII does not support characters in your name, Unicode will provide a solution.
Hexadecimal and Unicode
- ASCII uses 7 bits, limiting its range.
- To represent a broader range of characters, more bits are needed.
- Hexadecimal, or hex, is used in Unicode to represent these characters efficiently.
What is Hexadecimal?
- Hexadecimal is a base-16 number system.
- Hex digits include: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
- In programming, hex is encountered more often than binary for compactness.
Hex to Binary Mapping
Each hex digit corresponds to 4 binary bits:
- 0000 = 0
- 0001 = 1
- 0010 = 2
- …
- 1110 = E
- 1111 = F
One hex digit represents 4 bits, making it a shorthand for binary.
This is due to the fact that four binary digits can represent sixteen possible values (\(2^4\)), which aligns with the sixteen possible values of a single hex digit (0 to F).
Binary to Hex Conversion
- Convert binary to hex by grouping into blocks of four bits.
- Example: Binary
1001 1110 0000 1010converts to Hex9E0A.
Practice Exercise
Convert the decimal number 13 to binary.
Convert the decimal number 13 to hexadecimal.
Practice Exercise
Now, convert the decimal number 27 to binary and then to hexadecimal.
Hexadecimal in File Formats
- Files in hex format are often referred to as “binary” files.
- This terminology is due to the direct conversion between hex and binary.
- The conversion is unambiguous, making it a practical shorthand.
Hexadecimal in HTML
HTML uses hexadecimal to represent colors.
Six-digit hex numbers specify colors:
- FFFFFF = White
- 000000 = Black
Each pair of digits represents a color component (RGB).
Each color channel typically has a range from 0 to 255 (in 8-bit systems), which gives a total of 256 intensity levels for each primary color.
When you combine the three channels, you get a possible color palette of \(256^3\) or about 16.7 million colors.
For example, an RGB value of 255, 0, 0 corresponds to bright red because the red channel is at full intensity, and the green and blue channels are off.
Understanding Unicode and UTF-8
Encountering Unicode
Encountering a
UnicodeDecodeErrorin Python indicates a character encoding issue.This often arises when dealing with characters not represented in the ASCII set.
What is Unicode?
- Unicode is a standard that maps characters to code points.
- A code point is an integer, usually represented in hexadecimal.
- A Unicode string is a series of code points.
- Encoding is the rule set for converting code points to bytes.
ASCII and Unicode
- Unicode code points \(<\) 128 directly map to ASCII bytes.
- Code points \(>=\) 128 cannot be encoded in ASCII.
- Python will raise a
UnicodeEncodeErrorfor these cases. - Unicode code charts: Unicode Charts
UTF-8 Encoding
- UTF-8 stands for Unicode Transformation Format 8-bit.
- It is a variable-width encoding representing every Unicode character.
- Python uses UTF-8 by default for source code.
Example
To write “DAVI” in Unicode (UTF-8) using hexadecimal code points, you would use the Unicode code points for each character.
In UTF-8, the characters in the standard ASCII set, which includes uppercase English letters, are represented by the same values as in ASCII. The code points for ‘D’, ‘A’, ‘V’, and ‘I’ are as follows:
- “D”: “\u0044”
- “A”: “\u0041”
- “V”: “\u0056”
- “I”: “\u0049”
“DAVI” in Unicode (UTF-8) using these escape sequences would be represented as “\u0044\u0041\u0056\u0049”.
High vs Low-Level Languages and the Genesis of Programming
Zuse’s Computers

- Zuse’s computers, including Z1, Z2, Z3, and Z4, were designed to read binary instructions from punch tape.
- The logic of these machines was based on binary switching mechanisms (0-1 principle).
- Example: Z4 had 512 bytes of memory.
What is Assembly Language?
- Assembly language allows writing machine code in human-readable text.
- Early assembly programming involved writing code on paper, which was then transcribed to punch cards.
First Assemblers

- The first assemblers were human!
- Programmers wrote assembly code, which secretaries transcribed to binary for machine processing.
High and Low-Level Languages
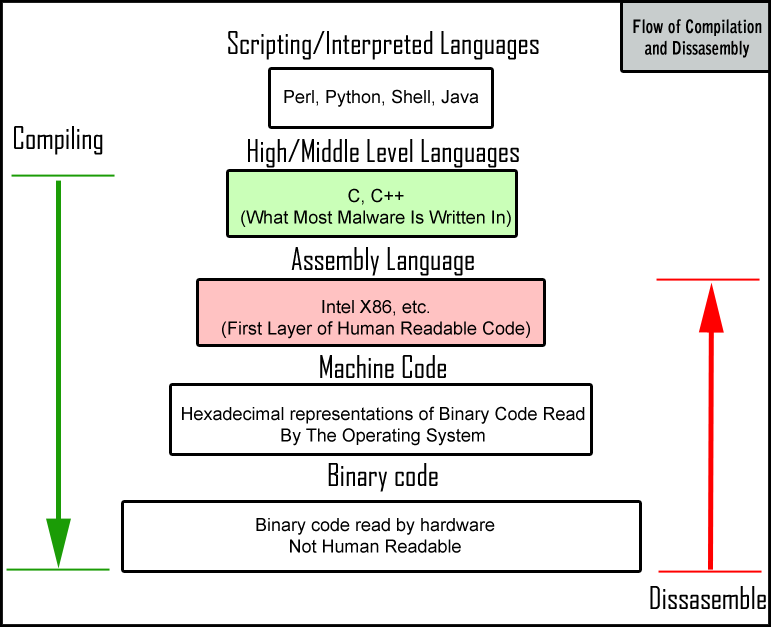
High-Level Languages: Abstract from hardware details, portable across different systems.
Low-Level Languages: Closer to machine code, require consideration of hardware specifics.
Compiled vs Interpreted Languages
Compiled Languages: Convert code to binary instructions before execution (e.g.,
C++,Fortran,Go).Interpreted Languages: Run inside a program that interprets and executes commands immediately (e.g.,
R,Python).
Performance and Flexibility
- Compiled languages are generally faster but require a compilation step.
- Interpreted languages are more flexible but can be slower, though this can be mitigated (e.g.,
PythonwithC++libraries).
Summary
Summary
- Computational Literacy: Binary and hexadecimal numbers, characters (ASCII, Unicode), and distinction between high vs low-level programming languages.
- Early Computing: Konrad Zuse’s pioneering work with programmable digital computers and the use of binary arithmetic.
- Assembly Language: The initial approach to programming using human-readable instructions for machine code.
- Calculators: The evolution from Leibniz’s four-species calculating machine to modern electronic computing.
- Silicon Microchip Computers: The 1970s revolution with transistors, integrated circuits, and the emergence of Von Neumann architecture.
- Modern Programming Languages: The spectrum from low-level assembly languages to high-level languages like
Python; distinction between compiled and interpreted languages.
Thank you!
Data Science Computing